Комплексная схема нечеткого планирования
Недостатком большинства известных в настоящее время систем планирования является их жесткая привязка к схеме планирования. Любая из них всегда ищет решение либо SS-проблемы, либо PR-проблемы. Связано это с фиксацией формы представления информации для планирования. Для классических моделей SS- и PR-проблем эти формы различны. Ясно, однако, что человек в своей деятельности успешно комбинирует шаги планирования из решения SS- и PR-проблем. Вторым недостатком является детерминированность систем планирования. В реальных ИС детерминированность планирования, как правило, не имеет места. Обобщение нечетких SS- и PR-проблем заключается в допущении нечетких состояний и нечетких операторов перехода из состояния в состояние. Разбиение задачи на подзадачи имеет весовые коэффициенты на дугах со значениями из [0, 1], которые интерпретируются как достоверности решения соответствующих подпроблем. Достоверность решения PR-проблемы определяется как минимум достоверностей решения ее подпроблем.
При переходе к обобщенной стратегии из решений нечетких подпроблем PR-проблемы, рассматриваемых как нечеткие SS-проблемы, можно получить решение нечеткой PR-проблемы, рассматриваемой также как нечеткая SS-проблема.
Схемой SS-проблемы называется пара M=(S,G), где S-множество состояний, G-множество отображений g: S->S, называемых операторами. Путем из состояния s0эS в состояние srэS называется конечная последовательность p=(( s0, , g0), (s1, g1),...,(sk-1, gk-1) sk ) , такая, что giO si= si+1 для i=0,..., k-1. SS-проблема-это четверка Р=(S, G, i ,f), где (S, G)-схема SS-проблемы, i, fэS-соответственно начальное и заключительное состояние. Путь х, ведущий из i в f, есть решение Р, а множество всех подобных путей составляет множество решений.
Схемой PR-проблемы называется пара .N=(S , Г), где S
-множество проблем, Г-множество отображений g : S ->S+, называемых операторами. Если РэS , p эS+, то gр(p)-отображение, представляющее проблему Р в виде цепочки подпроблем p = P1...Pn. Для схемы N=(S , Г) накрывающий путь q из проблемы s0 в конечное множество проблем Sk= {s1,...,sn} эS+ является конечной последовательностью, где q= ((x0 , y0), (x1, y1),..., (xk-1, yk-1), xk), xi э S+ для i=0,...,k, yэS+ для i=0,..., k-1, так что x0=s0, xkэS+k.
Подчеркнем, что как синтаксис, так и семантика подхода разбиения проблемы на подпроблемы не предполагают предварительного определения проблемы. Поэтому можно в качестве проблемы выбрать SS-проблему.
Рассмотрим понятие, объединяющее подходы разбиения проблемы на под-проблемы и поиска в пространстве состояний. 1-проблемой (объединенной проблемой) называется четверка R=(B, Г, Р0, Т), где В-множество SS-проблем;
(В, Г)-схема PR-проблем; Р0эB -основная проблема;T-импликативная сеть, такая, что WTЗB"Ж. Кроме того, R есть решение SS-проблемы Р0. Учитывая связь между существованием импликативной сети и разрешимостью проблемы, легко показать, что если для заданной I-проблемы найден накрывающий путь х из Р0 на множество Ф'Н В, проблемы Ф' разрешимы как SS-проблемы, если х частично представляет импликативную сеть Т, то и проблема R разрешима как SS-проблема.
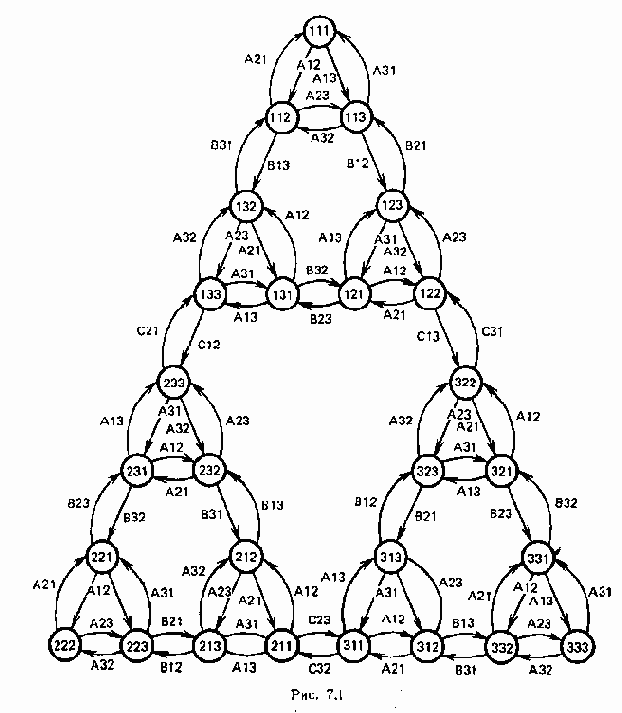
Рассмотрим головоломку "Ханойская башня" . Имеются три стержня 1, 2 и 3 и три диска различных размеров А, В, С с отверстием в центре, которые могут одеваться на стержни. В исходной позиции диски находятся на стержне 1; самый большой диск С-внизу, самый маленький диск А- наверху. Требуется перенести все диски на стержень 3, перемещая за один раз только один диск. Брать можно только самый верхний диск на стержне, причем его нельзя класть на диск, меньший по размерам. Используем для записи состояний и операторов классическую формализацию. Выражение ijk обозначает конфигурацию, при которой диск С находится на стержне i, диск В - на стержне j и диск А-на стержне k. Выражение xij обозначает действие, при котором диск х перемещается со стержня i на стержень j. С помощью этого формализма можно просто записать все состояния и переходы головоломки в виде треугольного графа, где вершины соответствуют расположению дисков на стержнях, а дуги-возможным перекладываниям дисков (рис.1). На этой головоломке легко проиллюстрировать все основные понятия обобщенной стратегии проблем.
Представим головоломку в виде модели I-проблемы.
Рассмотрим I-проблему R=(B, Г, P0T), где B={Р0, P1,...,P9}; Г={g }; T=={L1,L2,L3}. SS-проблемы Р0,P1..., P9 определяются следующим образом. На рис. 1 показана схема SS-проблемы M==(S, G), где
P0=(S, G, 111, 333), P1=(S, G, 111, 122), P2=(S, G, 122, 322),
Рз=(S, G, 322, 333), P4=(S, G, 111, 113), P5,=(S, G, 113, 123),
P6==(S, G, 123, 122), P7=(S, G, 322, 321), P8=(S, G, 321, 331),
P9=(S G, 331,333).
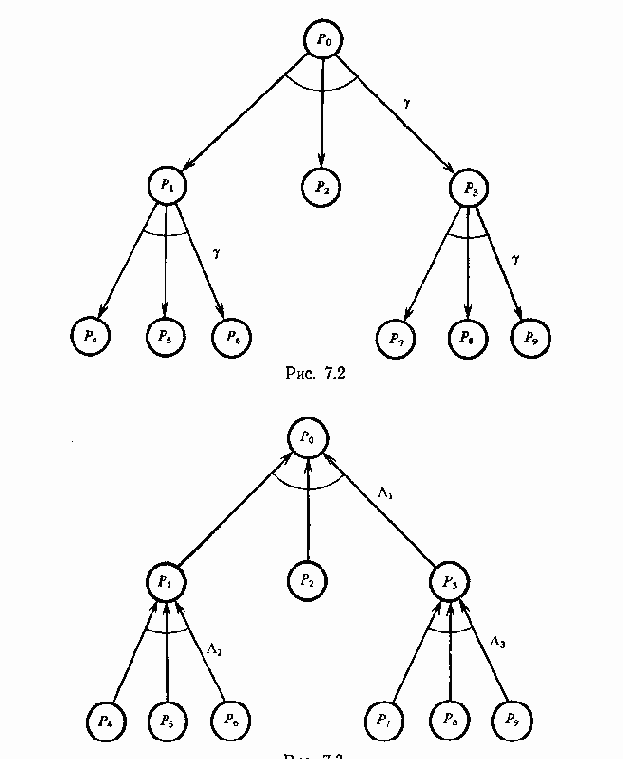
Схема PR-проблемы N= (В, Г) приведена на рис. 2; импликативная сеть Т- на рис.3, причем L1=(P0, P1Р2Р3, Y), L2= (P1, P4P5P6, Y), L з== (Р3, P7P8P9,Y ), где Y (x1,x2,x3)=x1x2x3.
Проблемы Р2 и P4-P9 решаются перекладыванием одного диска и являются элементарными. Проблемы P1 и Р3 решаются с помощью манипуляций только с дисками В и А и являются более простыми, чем Р0. Проблемы P1 и Р3 решаются, а проблема Р0 сводится к P1, P2 и Р3 аналогичной манипуляцией с дисками, синтаксис которой выражен оператором g, а семантика - отображением Y .
Представление этой головоломки в виде PR-проблемы (рис.2) является более компактным и наглядным, чем представление в виде SS-проблемы (рис.1), а представление в виде I-проблемы (рис..3) сочетает достоинство обоих и показывает взаимосвязь подпроблем и тех действий, которые нужно выполнить, чтобы решить головоломку.
Приведенные определения обобщаются на нечеткий случай, когда состояние системы, для которой строится модель решения проблемы, не является точно заданным, а результаты действий системы
неоднозначны.
Например,у робототехнической системы это может быть связано с несовершенством эф-фекторов и рецепторов, с ограниченными размерами внутренней модели, не отражающей сложности окружающего мира.
Нечеткой SS-проблемой назовем SS-проблему, у которой i , f-нечеткие множества, операторы g эГ-нечеткие матрицы, a-решением нечеткой SS-проблемы называется путь g=g1...gn,giэG,i=1,...,n, такой, что iOg1O... ... OgnOf? a , где О - максимальное произведение нечетких матриц.
Нечеткой PR-проблемой называется PR-проблема, у которой элементам g эГ приписывается степень принадлежности m g (p )э[0,1], a-решением нечеткой PR-проблемы называется решение PR-проблемы, для которой mingij? a,gij эyi.
Накрывающий путь в этом случае называется накрывающим a-путем. Степень принадлежности m g ( p ) интерпретируется как степень возможности разбиения проблемы на подпроблемы.
Нечеткой импликативной схемой называется импликативная схема, все отображения Y которой имеют степень принадлежности m Y ((p )э[0,1]. Степень принадлежности интерпретируется как возможность получения решения проблемы из решений соответствующих подпроблем. Нечеткой импликативной сетью называется импликативная сеть с нечеткими импликативными схемами.Нечеткая PR-проблема представляет нечеткую импликативную сеть, если кроме обычных условий для импликативной сети выполняется неравенство m Y (p )? m g (p ) ? a ,
т. е. возможность разбиения на подпроблемы не меньше возможности получения решения для каждой пары соответствующих Y и g.
Аналогично определяется нечеткая I-проблема. Но построить a-решение нечеткой PR-проблемы по a-решениям ее нечетких подпроблем можно лишь в частных случаях и при наложении дополнительных условий. Пусть задана нечеткая PR-проблема, где S-нечеткие SS-проблемы, и существует простейшее a-решение Z, т.е.такое p э S +,что m g p ? a,и если p =P1..Pn,то все проблемы Pi a-разрешимы,
где Pi=(Si,Gi,Ji,Fi ).a-решение проблемы P0 существует при m Y (p )? m g (p )? a для импликативной сети.Запишем более конструктивное условие для этого.Пусть для всех i оператор gi есть a-путь решения проблемы Piи Fi=Ji+1.Тогда,если выполняется max m [FnЗ (Fn-1З (...F1З (J o g1)o g2)...)o gn)]? a и g=g1...gn,то g- a-решение SS-проблемы P0.