ПРЕДСТАВЛЕНИЕ МНОЖЕСТВ С ПОМОЩЬЮ БИНАРНЫХ ДЕРЕВЬЕВ
Описание множеств в виде списков позволяет использовать для множеств целевое утверждение принадлежит, определенное ранее для списков.
Однако для множеств, состоящих из большого числа элементов, списковые целевые утверждения становятся неэффективными. Рассмотрим, например, как целевое утверждение принадлежит (см. предыдущий разд.) позволяет моделировать принадлежность множеству. Пусть L - список, описывающий множество из первых 1024 натуральных чисел. Тогда при ответе на запрос
?- принадлежит(3000, b).
Прологу придется проверить все 1024 числа, прежде чем заключить, что такого числа нет:
нет
Представление множества бинарным деревом позволяет добиться лучшего результата. При этом бинарное дерево должно быть упорядочено таким образом, чтобы любой элемент в левом поддереве был меньше, чем значение корня, а любой элемент в правом поддереве — больше. Поскольку мы определили поддерево как бинарное дерево, такое упорядочение применяется по всем поддеревьям. На Рис. 15 приведен пример упорядоченного бинарного дерева.
Дерево на Рис. 14 является неупорядоченным.
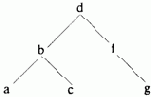
Рис. 15. Упорядоченное бинарное дерево.
Обратите внимание, что упорядочение приводит не к единственному варианту представления множества с помощью дерева. Например, на Рис. 16 изображено то же множество, что и на Рис. 15.
Будем называть линейным представление такого вида, как на Рис. 16, и сбалансированным - такое, как на Рис. 15.
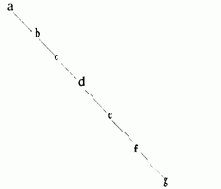
Рис. 16. Линейное представление.
Моделирование принадлежности множеству. Имея множество, описанное бинарным деревом, мы можем моделировать принадлежность множеству с помощью целевого утверждения принадлежит_дереву. При этом используется оператор @<, выражающий отношение «меньше, чем», и оператор @>, выражающий отношение «больше, чем».
/* Граничное условие: Х принадлежит
/* дереву, если Х является корнем.
принадлежит_дереву(Х, бд(Лд, Х, Пд)),
/* Рекурсивные условия
/* Х принадлежит дереву, если Х больше
/* значении корня и находится в правом
/* поддереве:
принадлсжит_дереву(Х, бд(Лд, У, Пд)) :- X@Y,
припадлежит_дереву(Х, Пд).
/* Х принадлежит дереву, если Х меньше
/* значения корня и находится в левом
/* поддереве:
принадлежит_дереву(Х, бд(Лд ,У ,Пд)) :-X@Y,
принадлежит_дереву(Х, Лд).
Если множество из первых 1024 чисел описать с помощью сбалансированного бинарного дерева Т, то при ответе на запрос
?- принадлежит_дереву(3000, Т).
Пролог сравнит число 3000 не более чем с 11 элементами множества. прежде чем ответит:
нет
Конечно, если Т имеет линейное представление, то потребуется сравнение 3000 с 1024 элементами множества.
Построение бинарного дерева. Задача создания упорядоченного бинарного дерева при добавлении элемента Х к другому упорядоченному бинарному дереву формулируется следующим образом:
Граничное условие:
Добавление Х к nil дает бд(nil, Х, nil).
Рекурсивные условия:
При добавлении Х к бд(Лд, К, Пд) нужно рассмотреть два случая, чтобы быть уверенным, что результирующее дерево будет упорядоченным.
1. Х меньше,чем К. В этом случае нужно добавить Х к Лд, чтобы получить левое поддерево. Правое поддерево равно Пд, а значение корня результирующего дерева равно К.
2. Х больше, чем К. В таком случае нужно добавить Х к Пд, чтобы получить правое поддерево. Левое поддерево равно Лд, а значение корня - К.
Такой формулировке задачи соответствует программа:
/* Граничное условие:
включ_бд(nil, Х, бд(nil, Х, nil)).
/* Рекурсивные условия:
/*(1)
включ_бд(бд(Лд, К, Пд), Х, бд(Лднов, К, Пд)) :-
Х@К,
включ_бд(Лд,Х,Лднов).
/*(2)
включ_бд(бд(Лд, К, Пд), Х, бд(Лд, К, Пднов)) :-
Х@К,
включ_бд(Пд, Х, Пднов).
На запрос
?- включ_бд(nil, d, Т1), включ_бд(Т1, а, Т2).
будут получены значения
Т1=бд(nil, d, nil)
Т2=бд(бд(nil, а, nil), d, nil)
Процедуру включ_бд() можно использовать для построения упорядоченного дерева из списка:
/* Граничное условие:
список_в_дерево([], nil).
/* Рекурсивное условие:
список_в_дерево([Н | Т], Бд) :-
список_в_дерево(Т, Бд2),
включ_бд(Н, Бд2, Бд).
Заметим, что включ_бд не обеспечивает построения сбалансированного дерева. Однако существуют алгоритмы, гарантирующие такое построение.